You bet on heads, the coin flips that way, and you win $1, bringing your equity up to $11. Each time you are successful, you continue to bet the same $1 until you lose. If you lose again, you’re down 3, so by doubling your bet again (4 chips), you might recoup your net loses and come out 1 chip ahead. Keep doubling until you win and then you’re back where you started, plus one shiny new chip. In this scenario you’re guaranteed to gain 1 chip if you keep playing.

Introduction

Not only do betting systems fail to beat casino games with a house advantage, they can’t even dent it. Roulette balls and dice simply have no memory. Every spin in roulette and every toss in craps is independent of all past events. In the short run, you can fool yourself into thinking a betting system works, by risking a lot to win a little. However, in the long run no betting system can withstand the test of time. The longer you play, the ratio of money lost to money bet will get closer to the expectation for that game.

In the many years that run this site, I have received thousands of e-mails from believers in betting systems. Their faith surpasses religious levels. However, in all things, the more ridiculous a belief is the more tenaciously it tends to be held. Gamblers have been looking for a betting system that works for hundreds of years, and yet the casinos are still standing.

Gambler's Fallacy

The biggest gambling myth is that an event that has not happened recently becomes overdue and more likely to occur. This is known as the “gambler’s fallacy.” Thousands of gamblers have devised betting systems that attempt to exploit the gambler’s fallacy by betting the opposite way of recent outcomes. For example, waiting for three reds in roulette and then betting on black. Hucksters sell “guaranteed” get-rich-quick betting systems that are ultimately based on the gambler’s fallacy. None of them work. If you don’t believe me here is what some other sources say on the topic:

A common gamblers’ fallacy called “the doctrine of the maturity of the chances” (or “Monte Carlo fallacy”) falsely assumes that each play in a game of chance is not independent of the others and that a series of outcomes of one sort should be balanced in the short run by other possibilities. A number of “systems” have been invented by gamblers based largely on this fallacy; casino operators are happy to encourage the use of such systems and to exploit any gambler’s neglect of the strict rules of probability and independent plays. — Encyclopedia Britannica (look under “gambling”)

No betting system can convert a subfair game into a profitable enterprise... — Probability and Measure (second edition, page 94) by Patrick Billingsley

The number of ‘guaranteed’ betting systems, the proliferation of myths and fallacies concerning such systems, and the countless people believing, propagating, venerating, protecting, and swearing by such systems are legion. Betting systems constitute one of the oldest delusions of gambling history. Betting systems votaries are spiritually akin to the proponents of perpetual motion machines, butting their heads against the second law of thermodynamics. — The Theory of Gambling and Statistical Logic (page 53) by Richard A. Epstein

Vegas Click also has a good expose of the gambler’s fallacy.

The Martingale

Every week I receive two or three emails asking me about the betting system by which a player doubles his/her bet after a loss. This system is generally played with an even money game such as the red/black bet in roulette or the pass/don’t pass bet in craps and is known as the Martingale. The idea is that by doubling your bet after a loss, you would always win enough to cover all past losses plus one unit. For example, if a player starts at $1 and loses four bets in a row, winning on the fifth, he will have lost $1+$2+$4+$8 = $15 on the four losing bets and won $16 on the fifth bet. The losses were covered and he had a profit of $1. The problem is that it is easier than you think to lose several bets in a row and run out of betting money after you’ve doubled it all away.

In order to prove this point, I created a program that simulated two systems, the Martingale and flat betting, and applied each by betting on the pass line in craps (which has a 49.29% probability of winning). The Martingale bettor would always start with a $1 bet and start the session with $255 which is enough to cover 8 losses in a row. The flat bettor would bet $1 every time. The Martingale player would play for 100 bets, or until he couldn’t cover the amount of a bet. In that case, he would stop playing and leave with the money he had left. In the event his 100th bet was a loss, he would keep betting until he either won a bet or couldn’t cover the next bet. The person flat betting would play 100 bets every time. I repeated this experiment for 1,000,000 sessions for both systems and tabulated the results. The graph below shows the results:

As you can see, the flat bettor has a bell curve with a peak at a loss of $1, and never strays very far from that peak. Usually the Martingale bettor would show a profit represented by the bell curve on the far right, peaking at $51; however, on the far left we see those times when he couldn’t cover a bet and walked away with a substantial loss. That happened for 19.65% of the sessions. Many believers in the Martingale mistakenly believe that the many wins will more than cover the few losses.

In this experiment, the average session loss for the flat bettor was $1.12, but was $4.20 for the Martingale bettor. In both cases, the ratio of money lost to money won was very close to 7/495, which is the house edge on the pass line bet in craps. This is not coincidental. No matter what system is used in the long run, this ratio will always approach the house edge. To prove this point consider the Martingale player on the pass line in craps who only desires to win $1, starts with a bet of $1, and has a bankroll of $2,047 to cover as many as 10 consecutive losses. The table below shows all possible outcomes with each probability, expected bet, and return.

Expand

Number of losses	Final outcome	Highest bet	Total bet	Net outcome	Probability	Expected bet	Expected return
0	Win	1	1	1	0.49292929	0.49292929	0.49292929
1	Win	2	3	1	0.24995001	0.74985002	0.24995001
2	Win	4	7	1	0.12674233	0.88719628	0.12674233
3	Win	8	15	1	0.06426732	0.96400981	0.06426732
4	Win	16	31	1	0.03258808	1.01023035	0.03258808
5	Win	32	63	1	0.01652446	1.04104089	0.01652446
6	Win	64	127	1	0.00837907	1.06414175	0.00837907
7	Win	128	255	1	0.00424878	1.08343900	0.00424878
8	Win	256	511	1	0.00215443	1.10091479	0.00215443
9	Win	512	1023	1	0.00109245	1.11757574	0.00109245
10	Win	1024	2047	1	0.00055395	1.13393379	0.00055395
10	Loss	1024	2047	-2047	0.00056984	1.16646467	-1.16646467
Total					1.00000000	11.81172639	-0.16703451

The expected bet is the product of the total bet and the probability. Likewise, the expected return is the product of the total return and the probability. The last row shows this Martingale bettor to have had an average total bet of 11.81172639 and an average loss of 0.16703451. Dividing the average loss by the average bet yields .01414141. We now divide 7 by 495 (the house edge on the pass line) and we again get 0.01414141! This shows that the Martingale is neither better nor worse than flat betting when measured by the ratio of expected loss to expected bet. All betting systems are equal to flat betting when compared this way, as they should be. In other words, all betting systems are equally worthless.

Here is another experiment I conducted earlier which proves the same thing as the experiment above. This one is played against roulette testing three different systems. Player 1 flat bet a $1 each time. He was not using a betting system. Player 2 started a series of trials with a bet of $1 and increased his wager by $1 after every winning bet. A lost bet would constitute the end of a series and the next bet would be $1. Player 3 also started a series of bets with a bet of $1 but used a doubling strategy in that after a losing bet of $x he would bet $2x (the Martingale). A winning bet would constitute the end of a series and the next bet would be $1. To make it realistic I put a maximum bet on player 3 of $200. Below are the results of that experiment:

Player 1

• Total amount wagered = $1,000,000,000
• Average wager = $1.00
• Total loss = $52,667,912
• Expected loss = $52,631,579
• Ratio of loss to money wagered = 0.052668

Player 2

• Total amount wagered = $1,899,943,349
• Average wager = $1.90
• Total loss = $100,056,549
• Expected loss = $99,997,018
• Ratio of loss to money wagered = 0.052663

Player 3

• Total amount wagered = $5,744,751,450
• Average wager = $5.74
• Total loss = $302,679,372
• Expected loss = $302,355,340
• Ratio of loss to money wagered = 0.052688

As you can see the ratio of money lost to money wagered is always close to the normal house advantage of 1/19 ≈ 0.052632. In conclusion, varying of bet size depending on recent past wins or losses makes no difference in the long run outcome and is no different than always betting the same.

A Third Experiment

“An Old Timer’s Guide to Beating the Craps Table” was a betting system that makes big promises about turning the craps tables into your own personal cash register. I offered to test his system for free. Here are the results.

The Cancellation Betting System

Despite all my warnings about betting systems, readers continually ask me to suggest one. To satisfy those who enjoy playing systems I have done a full explanation and analysis of the cancellation betting system.

Don't Waste Your Money

The Internet is full of people selling betting systems with promises of beating the casino at games of luck. Those who sell these systems are the present day equivalent of the 19th century snake oil salesmen. Under no circumstances should you waste one penny on any gambling system. Every time one has been put to a computer simulation it failed and showed the same ratio of losses to money bet as flat betting. If you ask a system salesman about this you likely will get a reply such as, “In real life nobody plays millions of trials in the casino.” You’re likely to also hear that his/her system works in real life, but not when used against a computer simulation. It is interesting that professionals use computers to model real-life problems in just about every field of study, yet when it comes to betting systems computer analysis becomes “worthless and unreliable,” as the salesman of one system put it. In any event, such an excuse misses the point; the computer runs billions of trials simply to prove that a system is unsound. If it won’t work on a computer, it won’t work in the casino.

Gambling systems have been around for as long as gambling has. No system has ever been proven to work. From an inside source, I know that system salesmen go from selling one kind of system to another. It is a dirty business by which they steal ideas from each other, and are always attempting to rehash old systems as something new.

System salesmen usually promise ridiculous advantages. For example, even with just a 1% advantage on an even money bet, it would not be difficult to parlay $100 into $1,000,000 by betting in proportion to bankroll. I was asked to prove this claim so I wrote a computer simulation based on the toss of a biased coin, with a 50.5% chance of winning. At all times the player bet 1% of his bankroll, rounded down to the nearest dollar. However, if a winning bet would put the player over $1,000,000 then he only bet as much as he needed to get to exactly $1,000,000. In addition, I ran simulations with a 2% advantage and for a starting bankroll of $1,000. Following are the results of all four tests.

$100 Bankroll, 1% Advantage

• Bets won = 7,182,811,698 (50.4999%)
• Bets lost = 7,040,599,544 (49.5001%)
• Player achieved $1,000,000 first = 79,438 (83.019%)
• Player went bust first = 16,249 (16.981%)
• Average number of bets to reach $1,000,000 = 174,972 (364.5 days at 8 hours per day, 60 bets per hour)

$100 Bankroll, 2% Advantage

• Bets won = 7,027,117,205 (51.0000%)
• Bets lost = 6,751,539,769 (49.0000%)
• Player achieved $1,000,000 first = 215,702 (98.099%)
• Player went bust first = 4,180 (1.901%)
• Average number of bets to reach $1,000,000 = 63,775 (132.9 days at 8 hours per day, 60 bets per hour)

$1,000 Bankroll, 1% Advantage

• Bets won = 5,213,026,190 (50.4999%)
• Bets lost = 5,109,817,544 (49.5001%)
• Player achieved $1,000,000 first = 74,818 (99.0285%)
• Player went bust first = 734 (0.9715%)
• Average number of bets to reach $1,000,000 = 137,208 (285.8 days at 8 hours per day, 60 bets per hour)

$1,000 Bankroll, 2% Advantage

• Bets won = 6,332,837,070 (50.9996%)
• Bets lost = 6,084,596,671 (49.0004%)
• Player achieved $1,000,000 first = 267,445 (99.9996%)
• Player went bust first = 1 (0.0004%)
• Average number of bets to reach $1,000,000 = 46,428 (96.7 days at 8 hours per day, 60 bets per hour)

These simulations prove that with just a small advantage of as little as 1% and a bankroll of as little as $100 you can grind your way to a million dollars through the gambling equivalent of compound interest. Yet you never hear of this actually happening. Could it be that these gambling systems don’t work after all?!

Here are some examples of system salesmen who try to take advantage of the mathematically challenged. There are hundreds of sites like these on the Internet, and this list is just a sampling. Frequently these sites vanish in the middle of the night, or suddenly direct traffic to a porn site. Please do let me know if any of these links don’t work or take you to other than the intended place.

Also, be warned that there are many others out there selling get rich quick gambling schemes that claim they are not betting systems. These sites usually throw out lots of fancy physics words like “chaos” and “fractals,” but display no evidence they know what these words mean. In the past, I have listed some such sites above but got angry letters claiming I shouldn’t criticize what I don’t understand. Personally, I feel that every method claiming an easy way to beat the casinos is a scam, and I don’t need to understand whatever the secret is. However, to be totally fair, I’ll only list betting systems above since those have been mathematically debunked by computer simulations. If anyone did find a truly easy way to beat the casinos, why aren’t they getting rich doing it?

The Wizard of Odds Challenge

For about six years, from 1999 to 2005, I offered $20,000 to anyone with a betting system that could show a profit over a one billion hand computer simulation. Here you can find the rules of the challenge. However, in all this time I only had one serious taker and hundreds of people wasting my time, pretending to be interested but never following through. So in January 2005, I took down the offer.

My webmaster, Michael Bluejay, now offers essentially the same challenge on his own site, VegasClick.com. If you accept his challenge, and win, I will be happy to state as such on the front page of this site, for proving the experts wrong.

A Fourth Experiment

On October 19, 2004, Daniel Rainsong accepted my challenge. Mr. Rainsong was so confident he would win he doubled the stakes to my $40,000 against his $4,000. Although the rules of the challenge are based on craps or roulette I allowed this challenge to be based on blackjack rules with a house edge of only 0.26%. Can a betting system beat a game with a house edge this small and a 1,028 bet spread? Visit my Rainsong Challenge page for all the details.

Please, Don't Write

I no longer respond to e-mails that suggest a player can beat a negative expectation game over the long run with a betting system. Such e-mail is deleted on sight. I have said all I have to say on the topic here and in my Gambling FAQ.

If you really want to discuss the topic, then I invite you not to do so at my forum at Wizard of Vegas, but instead one where you will be among like-minded people, like the forum atJohn Patrick's site (Update: This site has, not surprisingly, gone the way of the dodo bird).

Internal Links

• Oscar's Grind betting system.
• Labouchere betting system.
• Fibonacci betting system.
• Martingale betting system.
• D'Alembert betting system.
• Keefer roulette system.

Doubling Your Bet Strategy

External Links

• Betting Systems and the House Edge, an article by Ph.D. mathematician Eliot Jacobson debunking betting systems.
• Betting Systems, an article by Michael Bluejay of VegasClick.
• German translation of this article.
• Debunking the “No Risk Don’t Come” betting system.

Written by: Michael Shackleford

Roulette is one of the most popular table games in modern casinos. Although variations on the game have been around for several hundred years, there are now only 3 variations in American casinos.

You’re likely already familiar with American roulette and European roulette. The most recent addition to the table game inventory is Sands Roulette.

Which of these games should you play?

How should you bet on them?

What’s the smartest strategy for roulette betting?

I’ll explain all that in this post:

What Are the Differences between American, European, and Sands Roulette?

Although these games have a few other differences, the most significant distinction between the 3 versions of roulette are the number of green slots the wheels contain.

Every roulette wheel has at least 37 slots.

36 of those slots are always numbered 1 to 36, and they’re alternately colored RED or BLACK.

The additional slots are green.

In European roulette there is only one green slot, the “0”.

In American roulette there are two green slots: “0” and “00”.

In Sands roulette a third green slot, “S”, has been added to the wheel.

The green slots are there for one reason:

They make the game’s statistical probabilities uneven.

This is because of the way roulette bets are paid off. You can win anywhere from 35-to-1 (for betting on a single number) down to 1-to-1 (for betting on 18 slots at a time).

The payoffs, called “odds”, are not as fair to you as the actual estimated probabilities of the roulette ball landing on any given slot. This is how the casino makes its money.

In a game of roulette the house should keep at least 2.70% of all the bets players make over time. The casino has no need to cheat the players. In fact, the players often make really bad bets that improve the “house edge”, as that casino profit is called.

One of the other differences between European roulette and both American and Sands roulette is that the European roulette table has an additional betting area. This secondary betting area is used to place specially designed bets. They are more complicated than the normal bets made in American and Sands roulette. I’m going to ignore this section of the table, because I’m going to show you how to place bets that have the best chances of paying off.

Is There a Winning System for Roulette?

Everyone who gets into roulette sooner or later starts to think about how they can “beat the system”.

I’m going to be honest here:

There is no way to do that.

The green slots on the wheel make it impossible for anyone, anywhere, to ever design a betting system that is guaranteed to win. If you really want to guarantee yourself a win every time, then put a chip on each of the 2-to-1 outside bets and on each of the green number bets.

That’s the only way you’ll be paid money every time the wheel spins.

You’ll also go broke.

You may have heard about a system called the Martingale System. It’s a popular betting system with new roulette players.

Experienced roulette players just turn their heads and roll their eyes when someone mentions the Martingale System. The only way you can make money with the Martingale System is to write a book about it and get people to buy your book.

Even that’s a gamble, though, because most people now know that the Martingale System promises more than it delivers.

Here’s how this system works:

You start out betting the minimum. If you lose, you double your bet. If you win on your doubled bet, you go back to betting the table minimum. If you lose again, you double the size of your bet again.

This sounds great to inexperienced bettors but the problem is that you’ll either run out of money or hit the table limit before you can recoup your losses as they add up.

The Martingale System is a sucker bet, plain and simple.

Every betting system in every form of gambling tries to leverage probability theory. The Martingale System and other roulette betting strategies also rely on probability estimates.

But there’s a flaw in the thinking behind these systems. If you account for the flaw you’ll be okay. You won’t always win but your expectations will be more reasonable.

The secret to not going broke when you gamble is to set reasonable expectations and maintain your self-discipline. You should never drink or take drugs when you gamble. They lower your inhibitions and impair your judgment.

You might as well just hand your money over to the casino at the cashier window and say “keep it” if you’re going to drink or do drugs when you gamble.

How Do Probabilities Work in Roulette?

Probability theory came out of statistics. It tries to give us rules by which to guess what happens next in any situation. The guesses are seldom accurate predictions. Sometimes the guesses work out, and sometimes they don’t. Gamblers love probability theory because they think it helps them pick the best betting strategies.

You’re actually more likely to double your money during a roulette session if you put all your money on a single bet. The more bets you place, the less likely it becomes to double your money.

That’s because every bet brings you close to the long term expectations. The closer you are to the short term, the more likely you are to get better than expected results.

In roulette, the probabilities are simple. The dealer spins the wheel and releases a ball that whirls around the outside of the wheel and finally settles in a slot. With only 37 slots on a European roulette wheel you have a 1-in-37 probability of the ball landing on a specific slot.

This probability never changes.

This probability is calculated on the basis of all the known possibilities.

What probability theory cannot do, however, is predict where the ball will stop.

Nor can it predict whether the ball will land on red, black, or green any number of times over the next 100 spins.

Nonetheless, a lot of gambling guides tell you that you have the best chances of winning if you do this because of such-and-such probabilities. And many of these guides warn you that there is no way to predict the future, but by setting the expectation that the ball will land on red about 47% of the time, these guides are making predictions and promises they cannot keep.

They’ll even back up their claims by talking about how to run computer simulations for 1 million spins of the wheel so that you see how often the ball lands on red, black, or green.

Does Doubling Your Bet Work

In the real world the Probability Fairy is always on vacation. She’ll never be there to wave her magic wand to make things happen the way experts say they should. The ball could land on red over the next 20 spins. Or it could land on black or green or some random mix of color combinations.

You have no way of knowing how many of the next [X] spins will turn out a certain way. Talking about probabilities in this way is just dishonest.

What you can do is look at the wheel and ask yourself how much it costs to bet on the largest possible set of numbers. The idea here is to get as much coverage as you can without losing money too fast.

But even if you cover every number on the wheel you’ll lose money.

So the only way to win in roulette–and this is completely random, never guaranteed–is to bet on less than all the numbers on the wheel.

You also want to play bets that pay better than even money. You can place a variety of bets, but most of them aren’t worthwhile.

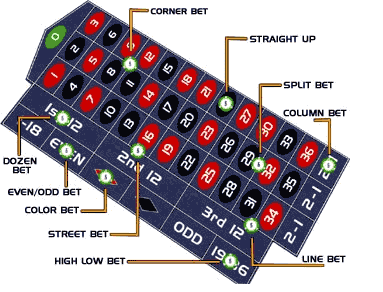
Betting on single numbers is a bad idea. You can place bets on the lines between the numbers (these are called “street bets”) and on lines at the corners of numbers (these are called “corner bets”).

But even though you get pretty good odds (payoff) you’re still covering too few numbers.

How Bets Work in Roulette

Divide the bets into two groups:

1. Inside bets
2. Outside bets

Inside bets are based on individual numbers or small groups of numbers. When you see players betting on the lines, corners, and individual numbers on the table they are making inside bets.

Outside bets are based on pre-selected groups of numbers on the wheel. The “2-to-1” bets cover 12 numbers each: 1 to 12, 13 to 24, and 25 to 36. The “1-to-1” or “even money” bets cover 18 numbers each:

• Odd
• Even
• Black
• Red
• 1 to 18
• 19 to 36

The bets more likely to pay are the even money bets.

But unless you can win 5 times out of 9 on even money bets you’ll lose your stake. That’s the problem with roulette. You always have to win at least 1 more time than you lose no matter how you place your bets.

The “2 to 1” bets pay better than the “1 to 1” bets because they cover fewer numbers. You have less of a chance of winning.

There are 6 types of “2 to 1” bets:

• 3 kinds of dozens bets: (1 to 12, 13 to 24, and 25 to 36)
• 3 kinds of columns bets: ([1, 4, 7, 10, 13, 16, 19, 22, 25, 28, 31, 34], [2, 5, 8, 11, 14, 17, 20, 23, 26, 29, 32, 35], [3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36]).

You can make a bet by betting on any two of the “2 to 1” groups. That means that instead of covering only 18 numbers you’ll be covering 24 numbers.

This type of bet is often called the “double dozen” bet. It’s popular among gamblers who like to hedge their bets. They have a better chance (all other things considered) of scoring a win with a “double dozen” than with one of the standard even money bets. If you’re playing it safe and going for even money odds, you should always play a double dozen bet.

If you want to bet more aggressively, then instead of betting more money on your double dozen, you can cover all 36 of the red and black numbers. Leave the green numbers alone. Yes, they’ll come in every now and then, and you’ll lose money.

But there’s a way to keep your losses low.

How to Bet on Columns or Dozens Aggressively

Take 6 chips and distribute them across EITHER the three dozen bets or the three column bets.

Place 3 chips on 1, 2 chips on the 2nd, and 1 chip on the 3rd. If the ball lands on a green number you’ll lose your entire bet, so always play the table minimum with this aggressive style.

If the ball lands on any number with your single chip bet, you’ll win 2 chips and lose 5–for a net loss of 3 chips (half your bet).

That’s the safest way to bet aggressively on the table.

If the ball lands on any number in your 2 chip bet you’ll win 4 chips and lose 4 for no loss. This keeps you in the game.

If the ball lands on any number in your 3chip bet, you’ll win 6 chips and lose 3 for a net gain of 3 chips. This will offset 1 single chip win.

The way this betting strategy works out, your money can grow substantially and still take some big hits. Where the strategy will fail you is when the ball lands on green or if the ball lands on the single chip bet more often than it lands on the 3 chip bet.

Sorry, but there’s no way to prevent that from happening.

There Is No Guaranteed Way to Win in Roulette

I can’t say this often enough:

You can’t win at roulette in the long run.

I think roulette is a fun game to play. It’s exciting because you don’t know where the ball will land. You take an active role in making your wagers.

And you’ll find there are a lot of different betting systems to experiment with. The only thing that is guaranteed in roulette is that the casino will make a profit. What you hope for is that they make their profit at someone else’s expense.

Players who try to improve their luck by making big bets do sometimes win, but most often the people who come out ahead are the patient players who use conservative betting strategies and take money off the table. If you only walk away with your beginning stake you’ll be luckier than most gamblers.

And you can take that to the bank.